Overview

The approach of Multi-Dimensional Homomorphisms (MDH) is an algebraic formalism for systematically reasoning about de-composition and re-composition strategies of data-parallel computations (such as linear algebra routines and stencil computations) for the memory and core hierarchies of state-of-the-art parallel architectures (GPUs, multi-core CPU, multi-device and multi-node systems, etc).

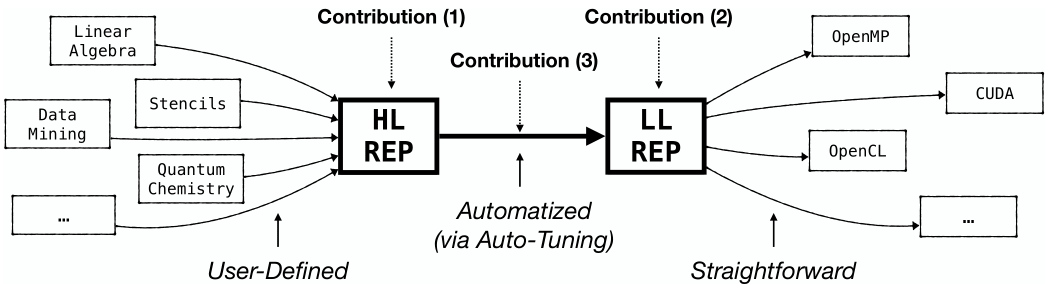
The MDH approach (formally) introduces:

  1. High-Level Program Representation (Contribution 1) that enables the user conveniently implementing data-parallel computations, agnostic from hardware and optimization details;
  2. Low-Level Program Representation (Contribution 2) that expresses device- and data-optimized de- and re-composition strategies of computations;
  3. Lowering Process (Contribution 3) that fully automatically lowers a data-parallel computation expressed in its high-level program representation to an optimized instance in its low-level representation, based on concepts from automatic performance optimization (a.k.a. auto-tuning), using the Auto-Tuning Framework (ATF).

The MDH’s low-level representation is designed such that Code Generation from it (e.g., in OpenMP for CPUs, CUDA for NVIDIA GPUs, or OpenCL for multiple kinds of architectures) becomes straightforward.

Overview of MDH Approach

Our Experiments report encouraging results on GPUs and CPUs for MDH as compared to state-of-practice approaches, including NVIDIA cuBLAS/cuDNN and Intel oneMKL/oneDNN which are hand-optimized libraries provided by vendors.

Ultimate MDH Goals

  • Performance: achieve performance competitive to hand-optimized solutions
  • Portability: target any kind of parallel architecture
  • Productivity: free user from hardware and optimization details


Getting Started

(Our implementation of MDH will be open sourced on GitHub)


Code Examples

From the following code examples, our MDH compiler generates fully automatically device- and data-optimized, executable program code, e.g., in OpenMP for CPUs, CUDA for NVIDIA GPUs, or OpenCL for multiple kinds of architectures.

MDH’s Python-Based User Interface

  • Matrix-Vector Multiplication (MatVec) expressed in MDH’s high-level program representation:

    def matvec(T: ScalarType, I: int, K: int):
    @mdh()
    def mdh_matvec():
        @scalar_function(
            out_scalar_type=[T],
            inp_scalar_type=[T, T]
        )
        def mul(out, inp):
            out['w'] = inp['M'] * inp['v']

        def scalar_plus(res, lhs, rhs):
            res['w'] = lhs['w'] + rhs['w']

        return (
            out_view[T]( w = [lambda i, k: (i)] ),
              md_hom[I, K]( mul, ( cc, pw(scalar_plus) ) ),
                inp_view[T, T]( M = [lambda i, k: (i, k)] ,
                                v = [lambda i, k: (k)   ] )
        )

    The above defined matvec function is used as follows:

    # MatVec on 1024x1024-sized input matrix and 1024-sized vector (both containing fp32 values)
matvec__fp32__1024_1024 = matvec( fp32, 1024,1024 )

# ... (CUDA host code: create CUDA context, CUDA buffers for "M","v", "w", etc.)

# Get MDH "CUDA Module" for MatVec (using ATF-tuned optimizations)
cuda__matvec__fp32__1024_1024 = mdhc.tune( matvec__fp32__1024_1024, pyATF( CUDARuntimeProfiler(), evaluations(1000) ), CUDA() )

# MDH CUDA Module: compile & load CUDA code
a100_cuda__matvec__fp32__1024_1024 = cuda__matvec__fp32__1024_1024.compile( arch='compute_80' )

# MDH CUDA Module: run MatVec on M,v to obtain w
a100_cuda__matvec__fp32__1024_1024.run( w,M,v )

# MDH CUDA Module: destroy module
a100_cuda__matvec__fp32__1024_1024.destroy()

# ... (CUDA host code: destroying CUDA context, freeing CUDA buffers, etc.)

  • Jacobi-1D (Jacobi1D) expressed in MDH’s high-level program representation:

    def jacobi1d(T: ScalarType, I: int):
    @mdh()
    def mdh_jacobi1d():
        @scalar_function(
            out_scalar_type=[T],
            inp_scalar_type=[T, T, T]
        )
        def f_j1d(out, inp):
            out['y'] = (inp['x', 1] + inp['x', 2] + inp['x', 3]) / 3.0

        return (
            out_view[T]( y = [lambda i: (i)] ),
              md_hom[I]( f_j1d, ( cc ) ),
                inp_view[T]( x = [lambda i: (i + 0),
                                  lambda i: (i + 1),
                                  lambda i: (i + 2)] )
        )

    The above defined jacobi1d function is used as follows:

    # Jacobi1D on a 1024-sized input vector (containing fp32 values)
jacobi1d__fp32_1024 = jacobi1d( fp32, 1024 )

# ... (CUDA host code: create CUDA context, CUDA buffers for "x", "y", etc.)

# Get MDH "CUDA Module" for Jacobi1D (using ATF-tuned optimizations)
cuda__jacobi1d__fp32_1024 = mdhc.tune( jacobi1d__fp32_1024, pyATF( CUDARuntimeProfiler(), evaluations(1000) ), CUDA() )

# MDH CUDA Module: compile & load CUDA code
a100_cuda__jacobi1d__fp32_1024 = cuda__jacobi1d__fp32_1024.compile( arch='compute_80' )

# MDH CUDA Module: run Jacobi1D on x to obtain y
a100_cuda__jacobi1d__fp32_1024.run( y,x )

# MDH CUDA Module: destroy module
a100_cuda__jacobi1d__fp32_1024.destroy()

# ... (CUDA host code: destroying CUDA context, freeing CUDA buffers, etc.)

MDH’s MLIR-Based User Interface

  • func.func @main()
{
  %M = memref.alloc() : memref<128x64xf32>
  %v = memref.alloc() : memref<64xf32>

  %w = mdh.compute "mdh_matvec"
  {
    inp_view =
    [
      [ affine_map<( i,k ) -> ( i,k )> ],
      [ affine_map<( i,k ) -> ( k )  > ]
    ],

    md_hom =
    {
      scalar_func = @mul,
      combine_ops = [ "cc", ["pw",@add] ]
    },

    out_view =
    [
      [ affine_map<( i,k ) -> ( i )> ]
    ]
  }
  {
    inp_types = [ f32, f32 ],
    mda_size  = [ 128,64 ],
    out_types = [ f32 ]
  }( %M,%v ) :
   ( memref<128x64xf32> ,
     memref<64xf32>     ) -> memref<128xf32>

  return
}

    Here, functions @mul and @add are straightforward, user-defined functions for computing scalar multiplication or scalar addition, respectively (both not shown for brevity). Functions cc and pw are pre-implemented combine operators for computing concatenation (cc) or point-wise operations (pw), respectively.

  • func.func @main()
{
  %x = memref.alloc() : memref<64xf32>

  %y = mdh.compute "mdh_jacobi1d"
  {
    inp_view =
    [
      [ affine_map<( i ) -> ( i+0 )> ,
        affine_map<( i ) -> ( i+1 )> ,
        affine_map<( i ) -> ( i+2 )> ]
    ],

    md_hom =
    {
      scalar_func = @jacobi,
      combine_ops = [ "cc" ]
    },

    out_view =
    [
      [ affine_map<( i ) -> ( i )> ]
    ]
  }
  {
    inp_types = [ f32 ],
    mda_size  = [ 62 ],
    out_types = [ f32 ]
  }( %x ) : (memref<64xf32>) -> (memref<62xf32>)

  return
}

    Here, function @jacobi is the Jacobi-specific computation (not shown for brevity), and cc is a pre-implemented combine operator for computing concatenation.

Automatic Parallelization & Optimization

Additionally, MDH supports as inputs – as an alternative to DSL programs in MDH’s high-level programming interface (shown above) – also straightforward (annotated) sequential program code. For our MatVec example, our Python-based input code is of the following form:

def matvec(T: ScalarType, I: int, K: int):
    @mdh( out( w = Buffer[T]                ) ,
          inp( M = Buffer[T], v = Buffer[T] ) ,
          combine_ops( cc, pw(add) )          )
    def mdh_matvec(w, M, v):
        for i in range(I):
            for k in range(K):
                w[i] = M[i, k] * v[k]

This program is completely equivalent to the DSL-based MDH program for MatVec shown above and used exactly the same:

# MatVec on 1024x1024-sized input matrix and 1024-sized vector (both containing fp32 values)
matvec__fp32__1024_1024 = matvec( fp32, 1024,1024 )

# ... (CUDA host code: create CUDA context, CUDA buffers for "M","v", "w", etc.)

# Get MDH "CUDA Module" for MatVec (using ATF-tuned optimizations)
cuda__matvec__fp32__1024_1024 = mdhc.tune( matvec__fp32__1024_1024, pyATF( CUDARuntimeProfiler(), evaluations(1000) ), CUDA() )

# MDH CUDA Module: compile & load CUDA code
a100_cuda__matvec__fp32__1024_1024 = cuda__matvec__fp32__1024_1024.compile( arch='compute_80' )

# MDH CUDA Module: run MatVec on M,v to obtain w
a100_cuda__matvec__fp32__1024_1024.run( w,M,v )

# MDH CUDA Module: destroy module
a100_cuda__matvec__fp32__1024_1024.destroy()

# ... (CUDA host code: destroying CUDA context, freeing CUDA buffers, etc.)

Schedule-Based Optimization Process

MDH optionally allows incorporating expert knowledge into the optimization process, using its scheduling language. By incorporating the user into the optimization process, we enable two major advantages over the standard MDH workflow:

  1. better optimization, as an auto-tuning system might not always make the same high-quality optimization decisions as a human expert
  2. faster auto-tuning, as some (or even all) optimization decisions might be made by the expert user and thus are not left to the costly auto-tuner
(An example scheduling program follows soon)


Publications

  1. A. Rasch
    (De/Re)-Composition of Data-Parallel Computations via Multi-Dimensional Homomorphisms
    ACM Transactions on Programming Languages and Systems (TOPLAS 2024)
    Paper Slides

  2. A. Rasch
    Full Version: (De/Re)-Composition of Data-Parallel Computations via Multi-Dimensional Homomorphisms
    arXiv 2024
    Paper Slides

  3. A. Rasch, R. Schulze, D. Shabalin, A. Elster, S. Gorlatch, M. Hall
    (De/Re)-Compositions Expressed Systematically via MDH-Based Schedules
    ACM SIGPLAN International Conference on Compiler Construction (CC 2023)
    Paper Slides

  4. A. Rasch, R. Schulze, and S. Gorlatch
    Generating Portable High-Performance Code via Multi-Dimensional Homomorphisms
    International Conference on Parallel Architectures and Compilation Techniques (PACT 2019)
    Paper Slides

  5. A. Rasch, R. Schulze, M. Gorus, J. Hiller, S. Bartholomäus, S. Gorlatch
    High-Performance Probabilistic Record Linkage via Multi-Dimensional Homomorphisms
    ACM/SIGAPP Symposium On Applied Computing (SAC 2018)
    Paper Slides

  6. A. Rasch, S. Gorlatch
    Multi-Dimensional Homomorphisms and Their Implementation in OpenCL
    International Journal of Parallel Programming (IJPP 2018)
    Paper

WIP/Short Papers & Talks

  1. A. Rasch, R. Schulze, Jens Hunloh, Lars Hunloh
    Code Generation & Optimization for Deep-Learning Computations via Multi-Dimensional Homomorphisms
    Compilers for Machine Learning (C4ML 2024), (lightning talk)
    Slides 1. Poster 2. Poster

  2. A. Rasch, R. Schulze, S. Gorlatch
    Array Programming via Multi-Dimensional Homomorphisms
    ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI 2023), (WIP paper)
    Paper Slides Talk

  3. R. Schulze, A. Rasch, S. Gorlatch
    Code Generation & Optimization for Deep-Learning Computations on GPUs via Multi-Dimensional Homomorphisms
    International Conference for High Performance Computing, Networking, Storage and Analysis (SC 2021), Best Poster Finalist, (short paper)
    Paper Poster Slides Talk

  4. A. Rasch, R. Schulze, S. Gorlatch
    Using MLIR for Multi-Dimensional Homomorphisms
    Google SIG MLIR Open Design Meeting 2020, (invited talk)
    Slides Talk

  5. A. Rasch, S. Gorlatch
    md_stencil: High-Performance Stencil Computations on CPU and GPU via Multi-Dimensional Homomorphisms
    International Conference on Parallel Architectures and Compilation Techniques (PACT 2020), (SRC – Gold Winner)
    Paper Poster Slides Talk

  6. A. Rasch, S. Gorlatch
    md_poly: A Performance-Portable Polyhedral Compiler Based on Multi-Dimensional Homomorphisms
    IEEE/ACM International Symposium on Code Generation and Optimization (CGO 2020), (SRC – Gold Winner)
    Paper Poster Slides

  7. A. Rasch, R. Schulze, S. Gorlatch
    Performance, Portability, and Productivity for Data-Parallel Applications on Multi- and Many-Core Architectures
    International Conference for High Performance Computing, Networking, Storage and Analysis (SC 2019), (doctoral showcase)
    Paper Poster Slides


Citations

Please use the following citations, when referring to MDH’s:

  1. Formalism & Design 
    @article{10.1145/3665643,
  author = {Rasch, Ari},
  title = {(De/Re)-Composition of Data-Parallel Computations via Multi-Dimensional Homomorphisms},
  year = {2024},
  publisher = {Association for Computing Machinery},
  address = {New York, NY, USA},
  issn = {0164-0925},
  url = {https://doi.org/10.1145/3665643},
  doi = {10.1145/3665643},
  journal = {ACM Trans. Program. Lang. Syst.},
  month = {may}}
  2. Scheduling Language 
    @inproceedings{10.1145/3578360.3580269,
author = {Rasch, Ari and Schulze, Richard and Shabalin, Denys and Elster, Anne and Gorlatch, Sergei and Hall, Mary},
title = {(De/Re)-Compositions Expressed Systematically via MDH-Based Schedules},
year = {2023},
isbn = {9798400700880},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
url = {https://doi.org/10.1145/3578360.3580269},
doi = {10.1145/3578360.3580269},
booktitle = {Proceedings of the 32nd ACM SIGPLAN International Conference on Compiler Construction},
pages = {61-72},
numpages = {12},
keywords = {GPU, scheduling languages, deep learning, CPU},
location = {Montr\'{e}al, QC, Canada},
series = {CC 2023}
}
  3. Automatic Parallelization and Optimization 
    @INPROCEEDINGS{mdpoly,
  author={Rasch, Ari and Schulze, Richard and Gorlatch, Sergei},
  booktitle={Proceedings of the International Workshop on Polyhedral Compilation Techniques (IMPACT 2020)},
  title={\texttt{md\_poly}: A Performance-Portable Polyhedral Compiler based on Multi-Dimensional Homomorphisms},
  year={2020},
  volume={},
  number={},
  pages={1-4}}


Contact

Avatar

Ari Rasch
Focus:Formalism
Affiliation:University of Münster
Email:a.rasch@uni-muenster.de
Website:arirasch.net
Avatar

Richard Schulze
Focus:Implementation
Affiliation:University of Münster
Email:r.schulze@uni-muenster.de
Website:richardschulze.net
Avatar

Lars Hunloh
Focus:MDH in MLIR
Affiliation:University of Münster
Email:l.hunloh@uni-muenster.de
Avatar

Jens Hunloh
Focus:MDH in MLIR
Affiliation:University of Münster
Email:j.hunloh@uni-muenster.de


You can also find us on Discord Discord.